Six Degrees of Freedom

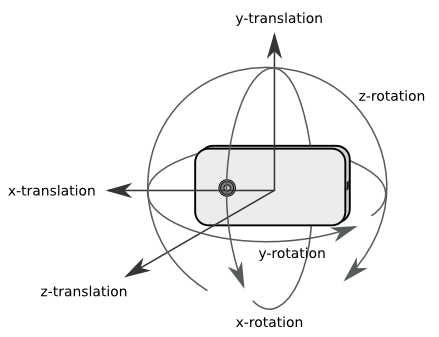
Our world consists of three dimensions - breadth, width, and height - and the word freedom refers to free movement in these three dimensions. In mathematics and engineering, we usually denote these three dimensions by x, y, and z.

By the word move, we mean both changing location by moving along an axis through space - known as translation, but also rotating about an axis while still remaining at the same coordinates. Consider how you would say you are moving when you are turning around, even though you’re standing on the same spot.

A smartphone and its camera has six degrees of freedom. Moving forward/backward, up/down, or left/right is called translation. Rotation around an axis is often termed pitch, yaw, or roll, depending on the axis of rotation. Since both intended and unintended movement in all six degrees of freedom can affect the recorded video, Vidhance has to understand, process, and cancel all six types of movement.

Accurate measurements of these movements are accomplished today through both AC and DC magnetic or electromagnetic fields in sensors that transmit positional and angular data to a processing unit and processed by Vidhance in real time.

Translation and rotation information can thus be provided by the smartphone’s sensors, or be inferred by Vidhance by tracking changes in the current scene, or both. Vidhance calculates the total movement and by changing the frame appropriately turns each frame in to the scene you intended. This is accomplished by separating the intended motion from the unintended motion, keeping only the former and cancelling the latter. For this to work, these movements must be expressed and analyzed mathematically.

Just as the complex numbers are a two-dimensional extension to the real numbers, quaternions are four-dimensional numbers. They can be added, subtracted, multiplied and divided according to their own special rules, which are compliant with the arithmetic rules of complex and real numbers. A rotation in 3D space can be represented numerically in several ways, for example with matrices or with unit quaternions.

Unit quaternions provide a more convenient mathematical notation for representing orientations and rotations of objects in three dimensions. They also have the advantage of being easier to compose, and compared to rotation matrices they are more numerically stable and may be more efficient.

Unit quaternions also avoid the problem of gimbal lock, where on degree of rotational freedom is lost when composing others. More precisely, gimbal lock is the loss of one degree of freedom in a three-dimensional, three-gimbal mechanism that occurs when the axes of two of the three gimbals are driven into a parallel configuration, “locking” the system into rotation in a degenerate two-dimensional space.